はじめに
今回は振り子の等時性(厳密)について紹介します。
皆さんは小学校5年生で振り子の等時性について実験した記憶はありませんか?
その際、ひもの長さが振り子の周期に影響を与えることを実験で確かめたと思います。
また、高校物理ではそれを数式を用いて証明しました。
これで振り子の等時性は完全に証明されたのでしょうか?
そんなことはありません。
高校物理の証明はあくまで近似的なものです。
では、厳密に解を導くとどのようになるのでしょうか?
実際に確かめてみましょう。
振り子の周期~高校物理~
最初に高校物理の証明をみていきましょう。
振り子を微小な角度\( θ \)で振らせます。
ひもの長さは\( l \)、おもりの重さは\( m \)で表します。
この時、運動方程式より以下のようになります。
$$ ma = -mgsinθ (2,1) $$
おもりの重さは\( m \)を消去して
$$ a = -gsinθ (2,2) $$
今、微小な角度で振り子を振らせることを考えています。
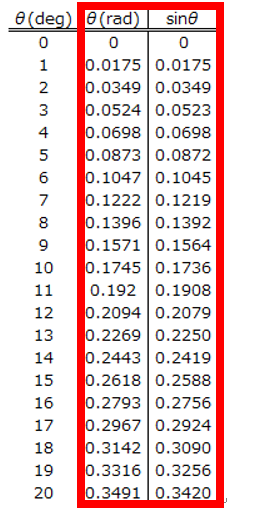
三角関数表を見てもらえると分かりますが、角度が微小な時は以下のような近似を行うことができます。
$$ θ ≓ sinθ $$
グラフで示すと次のような感じになります。
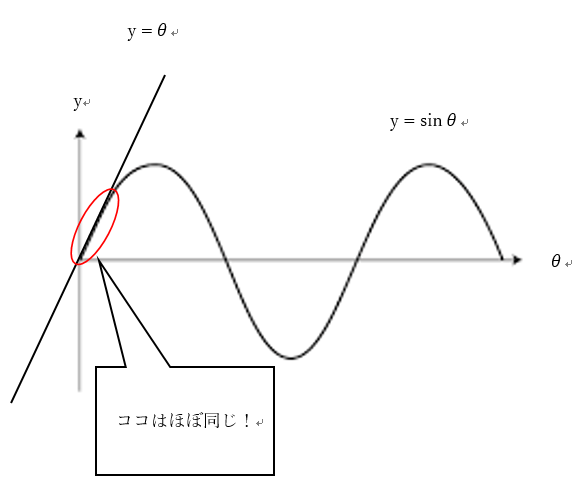
つまり(2,2)式は
$$ a = -gθ (2,3) $$
と近似的に表すことができます。
ここで弧度法を思い出しましょう。
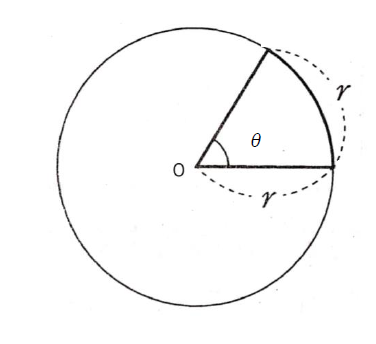
図のように、円の半径と弧の長さが等しくなる角度のことを1rad(ラジアン)と呼びます。
これを利用します。
ひもの長さ\( l \)が半径、\( x \)が弧の長さに対応します。
すると次のような式が成り立ちます。
$$ x = lθ $$
$$ θ = \frac{x}{l} $$
これを③に代入します。
すると
$$ a = -g\frac{x}{l} $$
$$ a = -\frac{g}{l} x (2,4) $$
このようになります。
これは単振動です!
単振動の公式より角速度\( ω \)として
$$ a = -ω^2x $$
(2,4)式と対応させると
$$ ω^2 = \frac{g}{l} $$
となります。
以上のことより
$$ ω^2 = \sqrt{\frac{g}{l}} (2,5) $$
となります。
単振動の周期を求める公式は
$$ T = \frac{2π}{ω} $$
より、(2,5)式に\( ω \)を代入して
$$ T = 2π\sqrt{\frac{l}{g}} $$
になります。
これは暗記している高校生も多いはずです。
この公式を見ると、変化する物理量はひもの長さ\( l \)しかありませんよね。
つまり、振り子の等時性はひもの長さによってのみ変化すると言うことができます。
これが高校物理までの内容です。
楕円積分
単振り子の周期を厳密に解ためには楕円積分の知識が必要なのでココで少し予習していきましょう。
楕円積分を解くと楕円関数が導かれます。
楕円関数とは二重周期を満たすような関数のことです。
楕円積分は3種類ありますが、今回はそのうちの2つを紹介します。
ヤコビの標準形
$$ E_k(x)= {\int_{0}^{x}\frac{dt}{\sqrt{(1 – t^2)(1 – k^2t^2)}}}dt - ① $$
$$ K_k(x)= {\int_{0}^{x}\sqrt{\frac{1 – k^2t^2}{1 – t^2}}}dt - ② $$
①が第一標準形の楕円積分、②が第二標準形の楕円積分とよばれるものです。
楕円積分にも形によって様々な呼び方があります。
上記の形はヤコビの標準形と呼ばれます。
次にルジャンドルの標準形と呼ばれる式を見てみましょう。
ルジャンドルの標準形
$$ F(k , φ)= {\int_{0}^{φ}\frac{1}{\sqrt{(1 – k^2sin^2θ)}}}dθ - ① (0≦k≦1) $$
$$ E(k , φ)= {\int_{0}^{φ}\sqrt{(1 – k^2sin^2θ)}}dθ - ② (0≦φ≦\frac{π}{2}) $$
ヤコビの標準形と同様に、①が第一標準形の楕円積分、②が第二標準形の楕円積分とよばれるものです。
上記の形はルジャンドルの標準形と呼ばれます。
特に\( φ = \frac{π}{2} \) のとき①と②式はそれぞれ、第一標準形の完全楕円積分、第二標準形の完全楕円積分と呼ばれます。
基本的に根号の中に三角関数が入っているときは、積分をすることはできません。
しかし、上記のような楕円積分と同様の形にもっていくことでコンピュータが数値計算しやすい形に帰着させてあげることはできます。
厳密には解くことはできませんのでご注意ください。
今、ヤコビの標準形とルジャンドルの標準形2つをご紹介しましたが、今回の振り子周期の厳密解を求めるに当たってはルジャンドルの標準形を使っていきます。
ちなみに楕円積分なんていう難しい名前になっているのは、第二標準形の楕円積分が楕円の円周を求める積分であることに起因しています。
なぜそれが第二標準形の楕円積分なのかは分かりませんが、、、
振り子の周期~第一標準形の完全楕円積分を用いた厳密解~
振り子の等時性を求める際には、第一標準形の楕円積分を使います。
高校物理の証明のどこが完璧では無いために厳密な解を求めることが出来ないのでしょうか?
それは微小な振れ角の部分です。
高校物理で証明する公式
$$ T = 2π\sqrt{\frac{l}{g}} $$
上記は微小な角度の時しか適用できない公式なのです。
微小って実際にどのくらいなのか?
だいたい0°~5°であれば上記の公式が適用できる範囲です。
それ以上の角度で振らせることを考える場合は、上記の公式では厳密には成り立たないのです。
それでは\( θ≓sinθ \)という近似をせずに計算を進めていきましょう。
まずは、振り子運動における力学的エネルギー保存の法則から出発しましょう。
図のような振り子の場合、次のようなエネルギー保存則の式が成り立ちます。
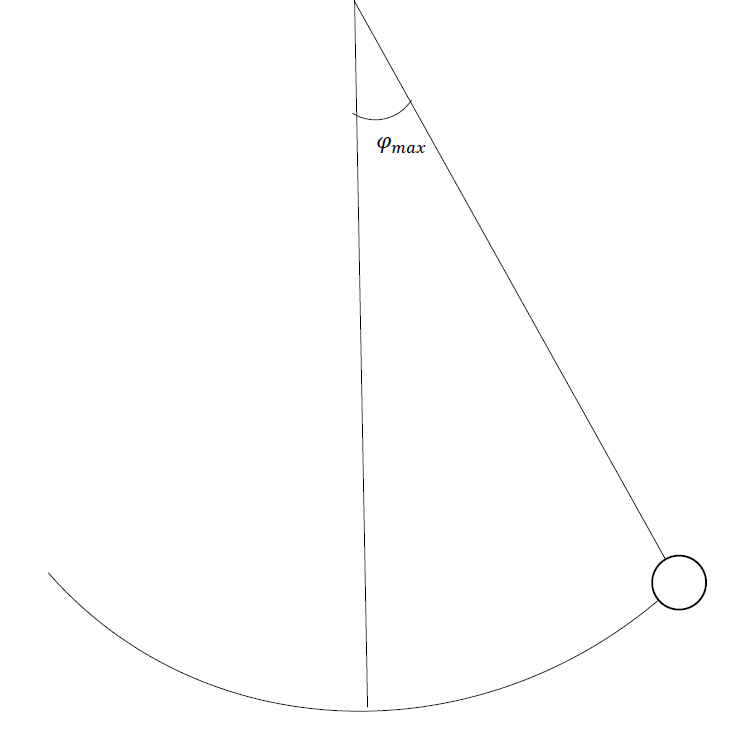
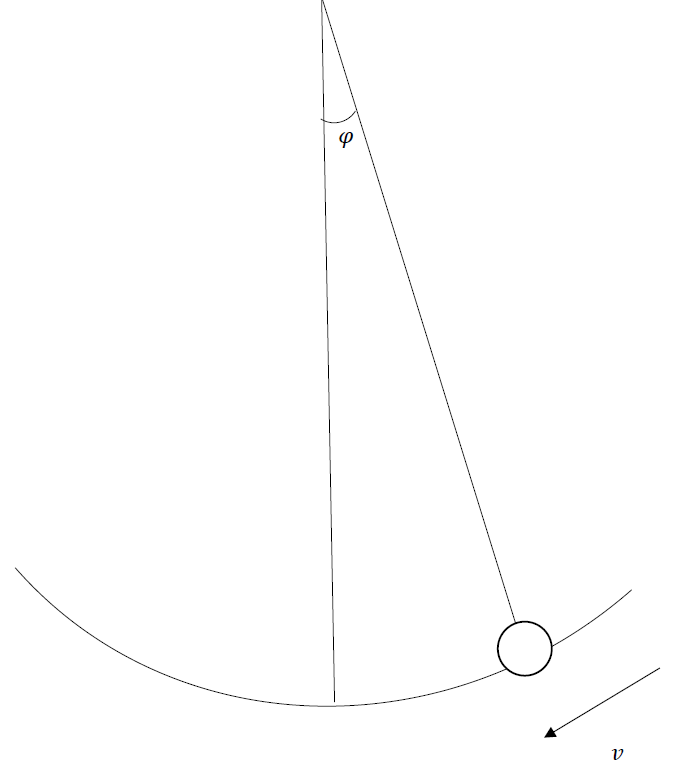
$$ \frac{1}{2}mv^2 – mg(lcosφ) = -mg(lcosφ_{max}) (4,1) $$
これはひもの付け根(一番上)を基準にしています。
ここで\( v = l \frac{dφ}{dt}(ω = \frac{dφ}{dt}) \)であるから(4,1)式に代入して
$$ \frac{1}{2}ml^2(\frac{dφ}{dt})^2 – mg(lcosφ) = -mg(lcosφ_{max}) $$
$$ (\frac{dφ}{dt})^2 = 2ω^2(cosφ – cosφ_{max}) (4,2) $$
$$ cosφ = 1 – 2sin^2(\frac{φ}{2}) $$
なので、(4,2)に代入して
$$ (\frac{dφ}{dt})^2 = 4ω^2(sin^2\frac{φ_{max}}{2} – sin^2\frac{φ}{2}) $$
根号を外すと
$$ \frac{dφ}{dt} = 2ω\sqrt{(sin^2\frac{φ_{max}}{2} – sin^2\frac{φ}{2})} (4,3) $$
おもりが\( t = 0 \)で最下点\( φ = 0 \)を通過するとして、最高点\( φ = φ_{max} \)に達する時間を(4,3)を用いて計算していきます。
$$ t = \frac{1}{2ω}{\int_{0}^{φ_{max}}\frac{dφ}{\sqrt{(sin^2\frac{φ_{max}}{2} – sin^2\frac{φ}{2})}}} (4,4) $$
ここで次のような変数変換を行います。
$$ sin\frac{φ_{max}}{2} = k(<1) (4,5) $$
$$ sin\frac{φ}{2} = ksinθ (4,6) $$
(4,6)式より
$$ cos\frac{φ}{2}\frac{dφ}{2} = kcosθdθ (4,7) $$
なので、次のようになります。
$$ dφ = \frac{2kcosθdθ}{cos(\frac{φ}{2})} $$
(4,6)式より
$$ cos\frac{φ}{2} = \sqrt{1 – k^2sin^2θ} $$
これを代入して
$$ dφ = \frac{2kcosθdθ}{\sqrt{1 – k^2sin^2θ}} $$
これを(4,4)に代入します。
$$ t = \frac{4}{ω}{\int_{0}^{\frac{π}{2}}\frac{dθ}{\sqrt{1 – k^2sin^2θ}}} $$
これはルジャンドルの標準形と同じ形していますよね。
$$ F(k , φ)= {\int_{0}^{φ}\frac{1}{\sqrt{(1 – k^2sin^2θ)}}}dθ - ① (0≦k≦1) $$
$$ E(k , φ)= {\int_{0}^{φ}\sqrt{(1 – k^2sin^2θ)}}dθ - ② (0≦φ≦\frac{π}{2}) $$
これを代入すると
$$ t = \frac{4}{ω}{\int_{0}^{\frac{π}{2}}F(k , φ)} $$
基本的に根号の中に三角関数がある場合は積分はできません。
何とか計算するために\( \frac{dθ}{\sqrt{1 – k^2sin^2θ}} \)を級数展開します。
$$ \frac{dθ}{\sqrt{1 – k^2sin^2θ}} = 1 + \frac{1}{2}k^2sin^2θ + \frac{1・3}{2・4} k^4sin^4θ + \frac{1・3・5}{2・4・6} k^6sin^6θ + ・・・ $$
以上より
$$ t = \frac{2π}{ω}\displaystyle\left\{1 + \displaystyle\left(\frac{1}{2}\right)^2k^2 + \displaystyle\left(\frac{1・3}{2・4}\right)^2k^4 + \displaystyle\left(\frac{1・3・5}{2・4・6}\right)^2k^6 + ・・・\right\} $$
この級数の第一項は角度\( φ_{max} \)が微小の場合に成り立ちます。
角度\( φ_{max} \)が大きくなるに従って、第二項、第三項と無視できなくなってきます。
\( φ_{max} \) が十分に小さいと近似すると\( T = 2π\sqrt{\frac{l}{g}} \)に帰着することを確認してみて下さい!
例えば、\( φ_{max} = 23° \)の場合は1%の誤差。
\( φ_{max} = 40° \)の場合は3%の誤差になります。
まとめ
今回は第一標準形の完全楕円積分を用いて振り子の周期を表す解を厳密に求めてみました。
$$ t = \frac{4}{ω}{\int_{0}^{\frac{π}{2}}\frac{dθ}{\sqrt{1 – k^2sin^2θ}}} $$
$$ t = \frac{4}{ω}{\int_{0}^{\frac{π}{2}}F(k , φ)} $$
これが振り子の周期の厳密解です!
かなり難しいですね。特に楕円積分はしっかり勉強しようとすれば本1冊買う必要があります。
イメージとしては、
振り子の周期を普通には求めることはできないので、コンピュータが計算しやすい形である楕円積分の形に式を帰着させた。そうすると数値計算をすることができた。
とういうような感じですね!
特に小学校で振り子の実験をやる先生には知っておいてほしいのですが、振り子の周期は厳密に言えば振れ角(角度)に依存します。
あくまで微小な振れ角(角度)においては依存しないということです。
小学生なんかは急に90°とかで振ったりするので注意が必要です。
私は大学時代に機械を使って実際にどのくらいの誤差が生まれるのかを確かめたことがあります。
振れ角40°と5°の差は0.051秒ほどでした。
下図が測定結果をグラフに示したものです。
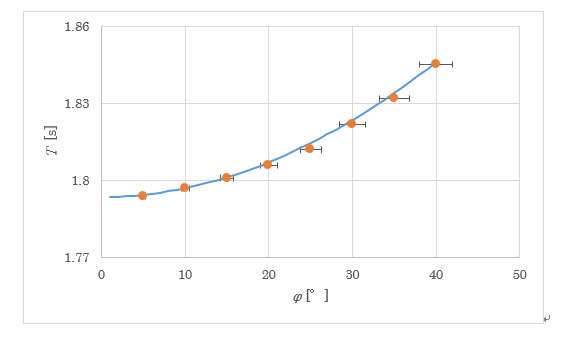
機械を用いてこの程度の差なので、小学生がストップウォッチ等を用いて測定する分には、誤差として処理することができると思います。
ただし、何度も言いますが振り子の周期は厳密に言えば振れ角(角度)に依存するということは知っておいてください。
今回の内容は以上です。
ココの分野をしっかりと学びたい人は、以下の本を参考に勉強してみてください!



コメント