はじめに
今回は物理基礎の開管についてです。
前回は、閉管についての気柱共鳴ということで、リコーダーなどの管楽器がどのように音を出しているのかを勉強しました。
今回も管楽器についてです。
違うのは、今回は両側の端が開いているということです。
振動数などの計算の仕方は前回の方法と全く同じです。
頑張っていきましょう!
気柱にできる定常波
気柱を伝わっていく音波は、気柱の両端で何度も反射します。
両側が開いていますが、気柱内と外部との圧力差が壁となり、音が反射します。
気柱の入り口からの入射波と端の反射波が定常波を作り共鳴します。
今回考える管には
- 閉管(片方が閉じている管)
- 開管(両方開いている管)
2種類あります。
今回は開管について考えましょう!
今回考える波は音波です。
そのため、縦波である音波を横波として表したような図になります。
閉管にできる定常波
気柱共鳴において、
- 閉口端(閉じている部分)→固定端反射
- 開口端(開いている部分)→自由端反射
ということになっていましたね?
開口端では、音波を伝える空気が自由に振動することができます。
そのため、開口端では自由端反射をします。
開口端では、音波を伝える空気が自由に振動することができます。
そのため、開口端では自由端反射をします。
弦の振動と同様に気柱共鳴にも種類があります。
これは振動数の違いによるものです(大事です)。
振動数が小さい振動から「基本振動」次に「2倍振動」次が「3倍振動」とどんどん増えていきます。
閉管と違い、順番に増えていきます。
閉管の振動数を表す公式は次のように表されます。
$$ f_n = \frac{v}{2L}×n(n=1,2,3・・・)- A $$
前回と同様にこれは覚えませんよ!
こんな式はその都度自分で立てることができるものなので、覚える必要はありません。
公式の導出について説明します。
基本振動
基本振動は図のような状態です。
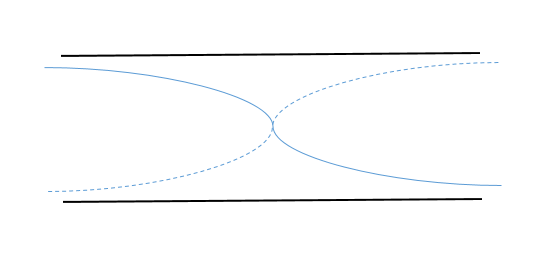
見にくいかもしれませんが、基本振動は1波長の2分の1ですよね。
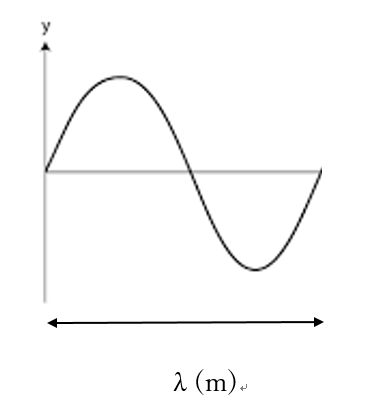
つまり \( \frac{1}{2}λ \) となります。 気柱の長さは\( L \)なので、次の式が成り立ちます。
$$ \frac{1}{2}λ = L $$
$$ λ = 2L $$
波の基本公式より
$$ v = fλ $$
\( λ=2L \)を代入して
$$ v = f・2L $$
振動数 \( f \) について求めると
$$ f_1 = \frac{v}{2L} $$
基本振動なので \( f_1 \) としています。
A式と見比べると、nに1を代入した式になっていますよね。
2倍振動
2倍振動は図のような状態です。

下図のように2倍振動はちょうど1波長ですよね。

つまり \( λ \) となります。 気柱の長さは\( L \)なので、次の式が成り立ちます。
$$ λ = L $$
波の基本公式より
$$ v = fλ $$
\( λ = L \)を代入して
$$ v = f・L $$
振動数 \( f \) について求めると
$$ f_2 = \frac{v}{L} $$
2倍振動なので \( f_2 \) としています。
A式と見比べると、nに2を代入した式になっていますよね。
3倍振動
3倍振動は図のような状態です。
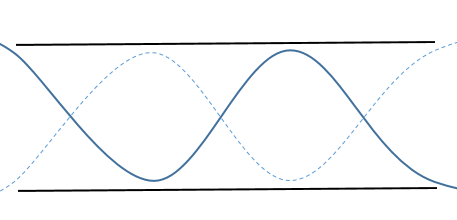
下図のように3倍振動は1波長と2分の1ですよね。

つまり \( \frac{3}{2}λ \) となります。 気柱の長さは\( L \)なので、次の式が成り立ちます。
$$ \frac{3}{2}λ = L $$
$$ λ = \frac{2}{3}L $$
波の基本公式より
$$ v = fλ $$
\( λ = \frac{2}{3}L \)を代入して
$$ v = f・\frac{2}{3}L $$
振動数 \( f \) について求めると
$$ f_3 = \frac{3v}{2L} $$
3倍振動なので \( f_3 \) としています。
A式と見比べると、nに3を代入した式になっていますよね。
次は4倍振動、5倍振動と増えていきます。
開口端補正
気柱共鳴は図のように管から少しだけ波がはみ出します。
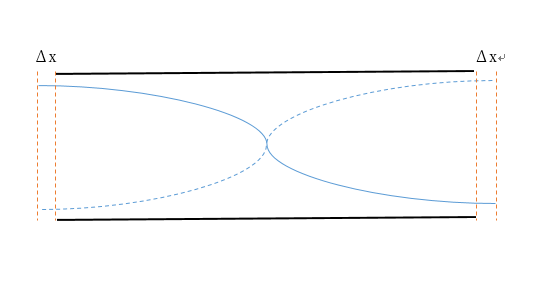
これは閉管のときと同じです。
これを開口端補正といいます。
問題文によっては開口端補正も考慮して計算する必要があります。
開口端補正はよく\( Δx \) と表記されます。
閉管と違って左右に現れることに注意しましょう。
では、基本振動を開口端補正も考慮して計算してみましょう。
つまり \( L+ 2Δx \) となります。
波長は\( \frac{1}{2}λ \)なので、次の式が成り立ちます。
$$ \frac{1}{2}λ = L + 2Δx $$
$$ λ = 2(L+2Δx) $$
波の基本公式より
$$ v = fλ $$
\ λ = 2(L+2Δx) を代入して
$$ v = f・2(L+2Δx)$$
振動数 \( f \) について求めると
$$ f_1 = \frac{v}{2(L+2Δx)} $$
まとめ
今日は開管の気柱共鳴について勉強しました。
弦の振動に関する公式が以下の公式です。
$$ f_n = \frac{v}{2L}×n(n=1,2,3・・・) $$
この公式は覚えるのではなく、自分で導出できるように練習しましょう!



コメント