今回は解析力学について勉強していきます!
解析力学に出てくるラグランジュ方程式はニュートンの運動方程式をより一般化したものですが、ひたすら難しい数式との格闘です。
もちろんその奥にある本質的な部分は今後、物理学を学んでいく上で必要不可欠なものではあります。
しかし、初学者にとってはどうも分かりにくい!
そのため、今回の記事では解析力学のラグランジュ方程式の導出までを順を追って説明していきたいと思います。
最初に言っておきますが、これが解析力学の全てでは当然ありません。
取っ付きにくい人のための導入だと思ってもらえると幸いです。
それではいきましょう!
解析力学の歴史
本格的に学ぶ前に、まずは少し歴史を勉強しましょう。
幾何光学の分野では、反射と屈折の法則をまとめ、さらに媒質が連続的に変化している場合にまで拡張した法則として「フェルマーの定理」というものがあります。
この法則は
一定点から出て他の一定点に達する光の経路は、両端を固定したまま途中を連続的に微小変化して得られるすべての経路に比べて、光がそれを通過するときに要する時間が極小(または極大)になるようなものである
というものです。
また、このような法則を一般に「変分原理」と言います。
変分原理による力学の定式化は
自然界における現象はその現象が関係する”何かある積分”が極大または極小になるような経路で起こる
という原理で、全てを説明しようとする試みの一環です。
特にこの”何かある積分”を「作用積分」と言います。
このような背景は以下の参考書に詳しい記載があります。
汎関数
解析力学において特に変分原理を用いて式を表そうとするするとき「汎関数」の知識が必要になってきます。
「汎関数」とは①式の様に表される関数であり\( y = f(x) \)の関数形がどのようなものであるかによって違ってきます。
$$ I = {\int_{a}^{b} F(x,y,y’) dx} - ①$$
このとき、\( I \)は関数\( y = f(x) \)の汎関数であると言い、一般に\( I[y] \)という形で表します。
関数との違いは、\( x \)がある値をとった時に\( y \)がある値をとるものが関数であるのに対して、\( y \)の関数形によって\( I \)が異なる値をとるものが汎関数です。
分かりにくいですよね。
例を示します。
下図のような曲線の長さを求めることを考えます。
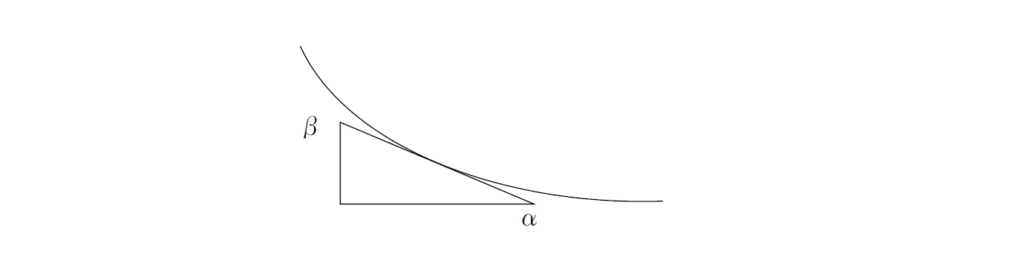
長さは\( \alpha \)から\( \beta \)までとして、三角形の縦と横はそれぞれ\( Δx \)と\( Δy \)とします。
そして曲線の長さを\( L \)とします。
すると三平方の定理より
$$ ΔL = \sqrt{(Δx)^2 + (Δy)^2} $$
両辺を\( dt \)で割ると
$$ \frac{dL}{dt} = \sqrt{\biggl( \frac{dx}{dt}\biggl)^{2} + ( \frac{dy}{dt}\biggl)^{2} } $$
よって\( x=t \)とおいて
$$ δf = \frac{∂f}{∂y}δy+\frac{∂f}{∂y’}δy’ $$
と表すことができます。
ここで
\( (\frac{dy}{dt})^{2} \)をよく\( y’ \)と表現されます。
曲線の長さ\( L \)は関数\( y \)(グラフ)によって変化するものであり、様々な変化がある中で\( L \)の最大・最小を考えるものが変分法と呼ばれる数学の手法です。
また、微分法との対応から\( L \)が停留値をとる時、\( δL = 0 \)となります。
(汎関数\( L \)は最小値をとるものだと考える。
最小値をとった\( L \)の変分\( δL \))は 0になります)
オイラーの方程式
上の例から、\( f \)を\( x,y,y’ \)の関数と考え、汎関数\( L \)が次の形で表されると考えます。
$$ L[y] = {\int_{α}^{β} f(x,y,y’) dx} - ②$$
ココで、下図のように終始の定点は固定し、経路を少しだけずらしたものを考えます。
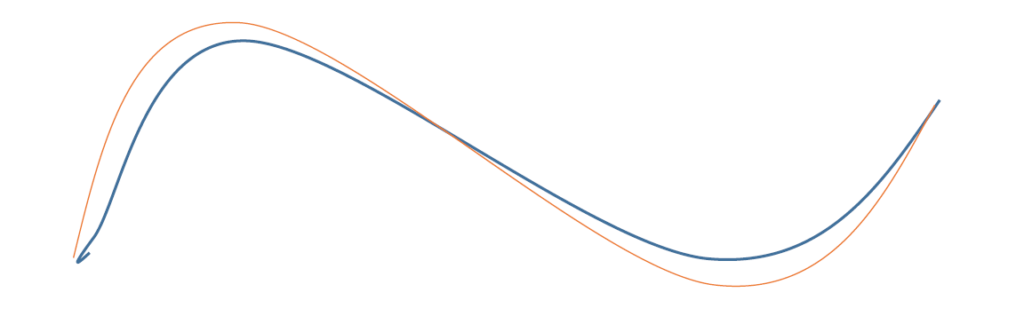
青線を\( L[y] \)、赤線を\( L[y+δy] \)とおきます。
そのため②式を用いて
$$ δL = {\int_{α}^{β} f(x+δx,y+δy,y’+δy) dx}-{\int_{α}^{β} f(x,y,y’) dx}=0 $$
$$ δL = {\int_{α}^{β} {f(x+δx,y+δy,y’+δy)-f(x,y,y’)} dx}=0 $$
ここで、カッコの中身は微分方程式の形と考えることができます。
そのため、全微分してあげると
$$ δf = \frac{∂f}{∂y}δy+\frac{∂f}{∂y’}δy’ $$
となるので
$$ δL = {\int_{α}^{β} (\frac{∂f}{∂y}δy+\frac{∂f}{∂y’}δy’)dx}=0 $$
ここで部分積分の知識を用いて
$$ {\int_{α}^{β}{\frac{∂f}{∂y}-\frac{d}{dx}(\frac{∂f}{∂y’})}δydx}=0 $$
上式の恒等式が成り立つためには\({\frac{∂f}{∂y}-\frac{d}{dx}\frac{∂f}{∂y’}}\)の部分が0である必要があります。
以上より
$${\frac{∂f}{∂y}-\frac{d}{dx}(\frac{∂f}{∂y’})}=0 $$
が成り立ちます。
この式をオイラー方程式と呼びます。
ラグランジュ方程式
物体が静止している時、全体として力ははたらいていないと考えます。
しかし様々な力が働いている場合でもその和が0であれば、その状況は個々の力がつり合っていると考えることができます。
このようなつり合いの状態を表すために、これらの力が働いている質点の位置rを仮想的に\( δr \)だけ動かしてみる。
すると、この時になされる仕事\( δW \)は③のように表すことができます。
$$ δW = δr・\sum_{i}F_i - ③$$
つまり、つり合いの状態では任意の微小な変位に対して仕事がゼロになると表現することができます。
これを「仮想仕事の原理」と言います。
仮想仕事の原理は役に立つ手法ですが、力のつり合いが成り立つ場合しか使うことができないという欠点もあります。
つまり、等速直線運動にしか適用できないということです。
この欠点を補うのが「ダランベールの原理」と呼ばれる原理です。
ダランベールの原理により、加速度運動している質点に対しても、仮想仕事の原理が適用できるようになります。
ニュートンの運動方程式は
$$ m\frac{d^2r(t)}{dt^2} = F $$
このように表すことができますが、上式を少しいじると④式になります。
$$ F – m\frac{d^2r(t)}{dt^2} = 0 - ④$$
これは、見かけ上力がつり合っているとみなすことができます。
よって、仮想仕事の原理と同様の方法で⑤式を導くことができるようになりました。
$$ (F – m\frac{d^2r(t)}{dt^2})・δr = 0 - ⑤$$
次に③式の仮想仕事の原理を用いて、最初にハミルトンの変分原理(最小作用の原理)を導いていきます。
$$ δW = \sum_{i=1}^f (F – m\ddot{x}) δx_i = 0 - ⑥$$
この左辺と中辺の作用積分を積分区間\( [t_1,t_2] \)での時刻\( t \)による積分を\( δI \)とおくと
$$ δI = {\int_{t_1}^{t_2}δWdt} = {\int_{t_1}^{t_2}\sum_{i=1}^f (F_i – m\ddot{x}) δx_i dt} = 0 - ⑦$$
⑦式のようにできるのは、オイラー方程式を導く際に汎関数\( L \)が最小値をとる時、\( L \)の変分\( δL \)は0になるということが言えるためです。
数学における変分原理を力学にも適用しようと試みたと考えることができます。
⑥式のように仮想仕事の原理における式の形は\( δW=0 \)となっており、変分が0であると考え、中辺を変形することで力学におけるオイラー方程式を導くことができます。
以下⑦式の中辺を変形していきます。
第1項と第2項をそれぞれ\( δI_1 \)\( δI_2 \)とおくと以下の式で表されます。
$$ δI_1 = {\int_{t_1}^{t_2}\sum_{i=1}^f F_i δ x_i dt} = 0 - ⑧$$
$$ δI_2 = {\int_{t_1}^{t_2}\sum_{i=1}^f (- m\ddot{x_i}) δx_i dt} = 0 - ⑨$$
\( δI_1 \)について
外力 \( F_i \) が保存力であるとすると 、ポテンシャルを \( U \) とおいて\( F_i =-\frac{∂U}{∂x_i} \) となります。これを⑧式に代入して
$$ δI_1 = {\int_{t_1}^{t_2}\sum_{i=1}^f (- \frac{∂U}{∂x_i}δx_i) dt} = 0 $$
カッコの中身はポテンシャル \( U \) の全微分となっているので
$$ δI_1 = -{\int_{t_1}^{t_2} δU dt} = 0 - ⑧’$$
\( δI_2 \)について
$$ δI_2 = -{\int_{t_1}^{t_2}\sum_{i=1}^f m\ddot{x_i} δx_i dt} = 0 $$
部分積分の公式を用いて
$$ δI_2 = δ{\int_{t_1}^{t_2}\sum_{i=1}^f \frac{1}{2}m\dot{x_i}^2 dt} = 0 $$
ここで \( \sum_{i=1}^{f}\frac{1}{2}m \dot{x}_{i}^{2}=T \) とおくと
$$ δI_2 = δ{\int_{t_1}^{t_2} T dt} = 0 - ⑨’$$
\( δI=δI_1+δI_2 \)なので
$$ δI = δ{\int_{t_1}^{t_2} (T – U) dt} = 0 $$
ここで\( T-U=L \)とおきます。\( L \)はラグランジアンと呼ばれます。
$$ δI = δ{\int_{t_1}^{t_2} L dt} = 0 - ⑩$$
となり、ここからオイラー方程式を導く手順でラグランジュ方程式⑪式を導くことができます。
$${\frac{∂L}{∂x_i}-\frac{d}{dx}(\frac{∂L}{∂\dot{x}_i})}=0 - ⑪$$
ちなみにラグランジアン\( L \) は 、位置・速度・時間の関数で \( L(q_i, \dot{q}_i, t) \) と表されます。
また、⑩式はハミルトンの原理(最小作用の原理)と呼ばれています。
ラグランジュ方程式を丁寧に導出している参考書は以下の本があります。是非、参考にしてみてください!
最後に
ハミルトンの原理では、位置を固定しているオイラー方程式とは違い、時間を固定した方程式となっています。
しかし、歴史的には到達時間を固定しない形での定式化(モーペルテュイの最小原理)もされています。
それでも
- ニュートンの運動方程式とすっきりとした対応関係があること
- 有用な変分原理は時間を固定するものであること
以上2つの理由から、ハミルトンの原理が現在では主流になっているようです。
この考え方は、解析力学だけでなく、電磁気学や量子力学の分野でも用いられるものです。
力学分野ではラグランジュ方程式の導出過程からラグランジアン\( L = T – U \)という関係式が導かれています。
電磁気学や量子力学でもラグランジアンの関係式を見つけることで、さらに深い考察ができるようになるのです。
今回の内容は以上です。
どうでしたか?やっぱり数学が少々面倒に感じますね。
この数学の難しさや面倒さが大学物理の最初の難関であると個人的には思っています。
今は難しく感じるかもしれませんが、やっているうちに慣れます(笑)
頑張って勉強しましょう!
最後まで読んでいただきありがとうございました。



コメント