電気抵抗　抵抗率をイメージでわかりやすく解説

はじめに

今回は電気抵抗について勉強していきます。

前回は、電気分野の基礎知識と電流について勉強しました。

今回はまず始めに皆さんが中学校で勉強したオームの法則からやっていきます。

オームの法則

オームの法則覚えていますか？

$$ V = RI $$

\( V \) が電圧、 \( R \) が抵抗、\( I \) が電流です。

オームの法則の意味としては、導線の両端の電圧と流れる電流の大きさに比例する。

抵抗 \( R \) は比例定数なんですね。

オームの法則を計算中心でしか使っていないと実感が湧かないですが、一次関数と同様に考えると分かりやすいですよね。

$$ y = ax $$

この時、\( a \) は「傾き」「比例定数」なんて呼んでいましたよね。

つまり、グラフにしたときに抵抗 \( R \)の値によってグラフの傾きが変化します。

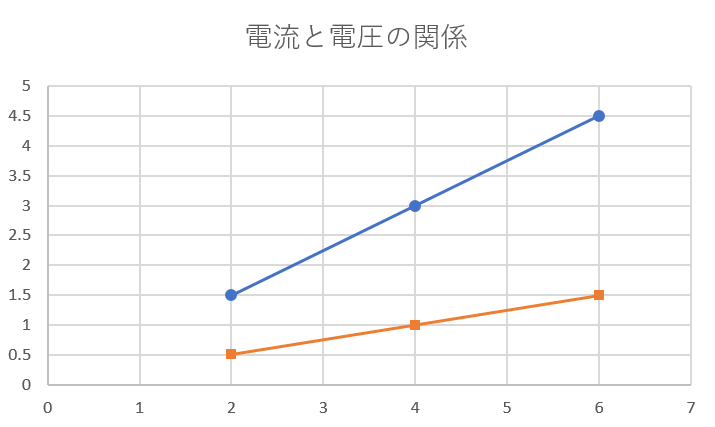
電流・電圧・抵抗のイメージ

前回の記事でも言いましたが、電気分野はイメージが難しいです。

現象や概念1つ1つのイメージがとても大切になってきます。

始めに電流・電圧・抵抗それぞれのイメージをもちましょう。

電流

電流は前回示したとおり、電子が動くことで発生します。

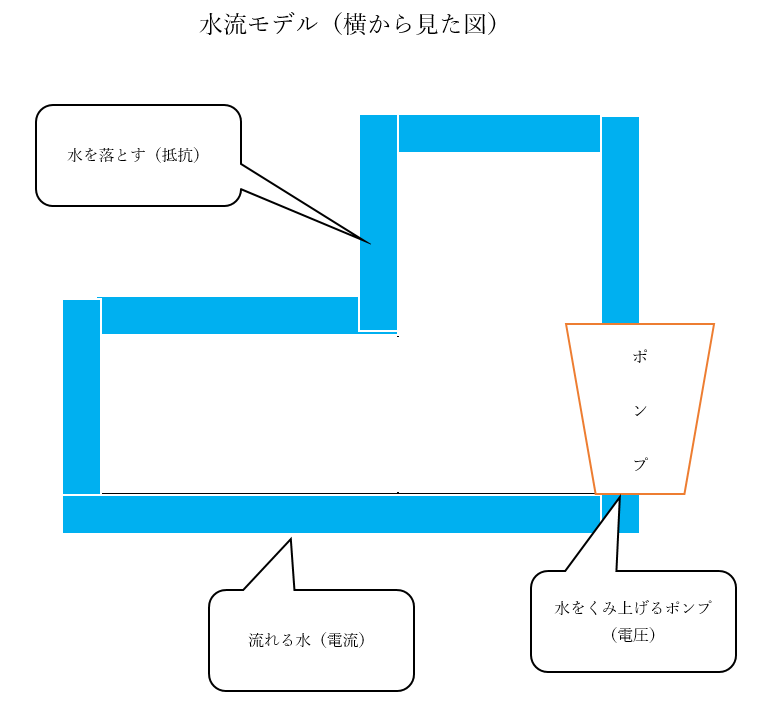
そんな電流ですが、水でイメージしましょう。

つまり、用水路などを流れている水が電流だと思うのです。

こういったイメージは水流モデルと呼ばれ、現象をイメージするためにはかなり有用なものです。

電圧

電圧のイメージに苦労する人が多いです。

電圧は、電流を流すために必要です。

回路を組む際に、電池や電源装置が電圧に当たります。

電圧のイメージは水をくみ上げるポンプです。

つまり電流である水をくみ上げ、流れるようにする役割を担っています。

電圧がなければ電流は流れないのです。

抵抗

抵抗は最初に説明したとおり、電圧と電流の関係式の比例定数になるものです。

抵抗は文字通り「邪魔する」ものです。

何を邪魔するのかと言えば、電流の流れです。

電流の流れを妨げるものだというイメージは持ちやすいのではないでしょうか？

しかし、水流モデルにおいては、ポンプである電圧がくみ上げた水（電流）を低い位置に落とすイメージをもちましょう。

このイメージは、後々に「物理」を勉強するときに役立ちます。

抵抗は、ポンプがせっかくくみ上げた水を元の高さに戻してしまうものと捉えましょう。

抵抗率

ここで抵抗についてもっと詳しく見ていきましょう。

抵抗 \( R \) を表す式は以下の通りになります。

$$ R = ρ\frac{l}{S} $$

それぞれの文字の意味を確認しましょう。

\( ρ \) は抵抗率、\( l \) は導線の長さ、\( S \) は導線の断面積を表しています。

抵抗率 \( ρ \) は、材質によって異なる比例定数です。

\( R = ρ\frac{l}{S} \) ですが、\( l \) と \( S \) どちらが分母でどちらが分子か分からなくなってしまうことありませんか？

覚えやすいイメージを今から教えます。

抵抗の原因

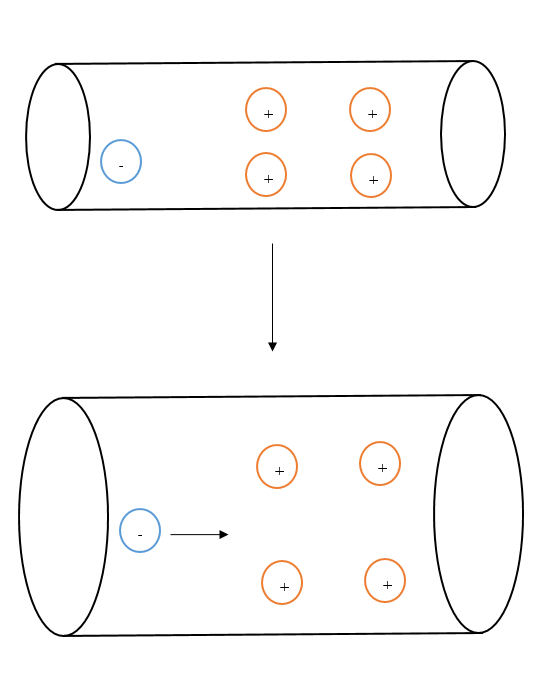
これは電流が流れる導線を拡大したものです。

そもそも抵抗はなぜ発生するのでしょうか？

物質は原子でできています。

原子の中心には陽子と中性子のある原子核がありますよね。

電圧によって動かされた電子がそういった原子核に衝突することによって、抵抗が発生します。

このとき、原子核は衝突の衝撃で振動します。

それが抵抗熱となって周囲を温めます。

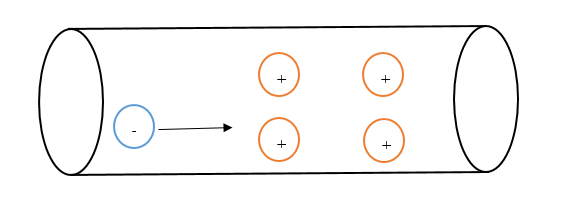
さて、\( R = ρ\frac{l}{S} \) のイメージですが、人混みをイメージしてください。

人が多くて混んでいる場所は、進みにくいですよね？

つまり、進もうとしているあなたが電流で、周囲の人が原子核です。

混み具合がひどければひどいほど進みにくいはずです。

例えば、そんな状態で1ｋｍ先を目指すのと2ｋｍ先を目指すのでは、どちらが大変でしょうか？

当然、2ｋｍ先を目指す方が大変なはずです。

そのため、導線の長さ \( l \) が分子になります。

長さが長くなればなるほど抵抗が増していきます。

次に、同じ混んでいる道を進むにしても、道幅が広ければどうでしょうか？

人が多くても、そこまで進みにくさは感じないはずです。

そのため、導線の断面積 \( S \) が分母になります。

断面積が大きくなればなるほど、抵抗が小さくなります。

様々な物質の電気抵抗率

これは前回の内容になります。

実はこれを表しているのが先にやった、抵抗率 \( ρ \) という物理量です。

例えば、鉄の抵抗率は約 \( 1.0×10^{-7} (Ω・ｍ)\) ですし、天然ゴムの抵抗率は役 \( 1.0×10^{13} (Ω・ｍ)\) です。

この中間の抵抗率を示す物質を半導体と呼びます。

半導体としては、ケイ素やゲルマニウムが有名ですが、これらは温度が上昇することで電子の一部が自由に動けるようになります。

こういった特性を活かして、現在の精密機器には必須の素材となっています。

半導体の詳しい構造や原理についてはここでは触れませんが、半導体の進歩は現在の科学技術の進歩に大きく貢献しているのです。

まとめ

今回は電気抵抗について勉強しました。

$$ V = RI $$

これはオームの法則でしたね。

その中の抵抗 \( R \) を表す式は以下の通りになります。

$$ R = ρ\frac{l}{S} $$

抵抗率は物質によって変化する値で、大きく次のように分類されます。