直列接続と並列接続　公式の導出

はじめに

今回は抵抗のつなぎ方についてです。

中学校理科で合成抵抗の公式は習っているかと思います。

この講では、合成抵抗の公式を前回学習した抵抗のイメージをもとに求めてみたいと思います。

中学校での授業を忘れてしまっている人でも大丈夫です。

初めから分かりやすく解説していきます。

直列接続

直列接続とは、抵抗を1本の経路に複数接続した状態のことです。

今回は話を簡単にするために抵抗の数を2つにしておきます。

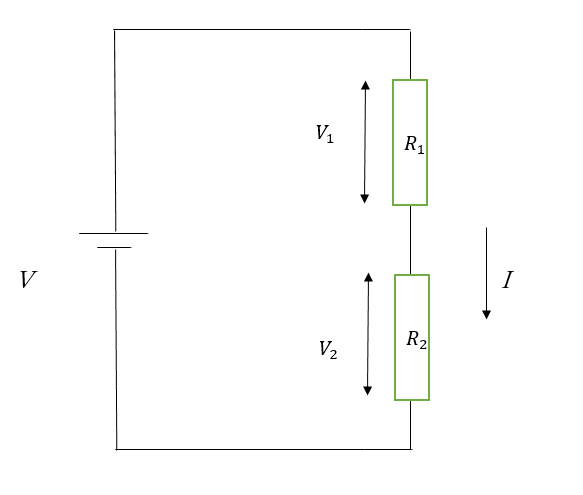
ここでも水流モデルで考えましょう。

電流は水、電圧はポンプ、抵抗は落下とイメージするんでしたね。

つまり次のような式が成り立ちます。

$$ V = V_1 + V_2 　　- ①$$

これは、ポンプ（電圧）で水をくみ上げた高さと、抵抗によって落とされた高さが等しいことを表しています。

図から見ても明らかですよね。

次に \( V_1 \) と \( V_2 \) それぞれをオームの法則を使って求めましょう。

オームの法則は次の式でした。

$$ V = RI $$

それぞれの抵抗を \( R_1 \) と \( R_2 \) とします。

導線は1本しか無いため、電流の値は常に同じです。

電流の大きさを \( I \) とします。

\( R_1 \) と \( R_2 \) それぞれの抵抗についてオームの法則より式を立てると

$$ V_1 = R_1 I 　　- ②$$

$$ V_2 = R_2 I 　　- ③$$

①に②と③をそれぞれ代入します。

$$ V = R_1 I + R_2 I $$

$$ V = (R_1 + R_2) I $$

以上より、直列接続の合成抵抗はそれぞれの抵抗を足すだけでいいことが分かりましたね。

抵抗の数が増えたときはその分追加で足すだけです。

並列接続

並列接続とは、抵抗を2本の経路に分け、枝分かれさせて複数接続した状態のことです。

直列接続の場合と同じ流れでいきましょう。

$$ V = V_1 = V_2 $$

これは、ポンプ（電圧）で水をくみ上げた高さと、抵抗によって落とされた高さが等しいことを表しています。

言っていることは同じですが、式が少し違いますよね？

並列の場合は、抵抗が横に並んでいるので、抵抗1つ分の高さしか落とされません。

今回は導線が枝分かれしているので、電流が同じではありません。

$$ I = I_1 + I_2 　　- ①$$

それぞれの抵抗を \( R_1 \) と \( R_2 \) とします。

オームの法則より、

$$ V = R_1 I_1 　　- ②$$

$$ V = R_2 I_2 　　– ③$$

①～③より

$$ I = I_1 + I_2 = \frac{V}{R_1} + \frac{V}{R_2} $$

$$ I = I_1 + I_2 = V(\frac{1}{R_1} + \frac{1}{R_2}) $$

以上より、並列接続における合成抵抗は逆数の足し算ということになります。

まとめ

今回は直列接続と並列接続の合成抵抗について説明しました。

電圧・電流・抵抗のイメージの大切さも分かっていただけたでしょうか？

何度も言いますが、物理基礎だけで無く物理に進んでから本当に大切になる考え方ですので、今のうちに身につけておいてください。