音の物理

はじめに

今回は音について勉強していきます。

以前の縦波・横波の回で音は縦波だと紹介しました。

そんな音波について見ていきましょう！

そもそも音とは

音は縦波だと言いました。それでは、音波の媒質は何でしょうか？

それは空気です。

音波とは、音源（音を発しているもの）の振動によって空気分子がビリヤードの玉突きのようにして我々の鼓膜に届き、聴神経から脳に伝達され、音として認識されています。

そのため、真空中では音は聞こえなくなります。

また、音源は例外なく振動しています。仏壇がある家は、仏壇の前に置いてあるお椀型のものがありますよね。宗教の流派によって呼び方が違うみたいですが「おりん」と言うそうです。

それを鳴らすと「カーーーン」と震えながら音を発生させます。この震えが振動です。

「おりん」が無い場合も、音楽機器やテレビなど音を発生させている電子機器に触ってみてください。

振動を感じられるはずです。

音の違いを決めるもの

皆さんは日常的に無意識にですが、様々な音を聞き分けていますよね。

「高い音や低い音」「大きい音や小さい音」「楽器による音の違い」

これらは音の3要素と呼ばれます。

それぞれをグラフで表すと次のようになります。

小さい音と大きな音は波の振幅の違い。

低い音と高い音は波の波長の違いが関係しています。

それぞれを見比べてみてください。

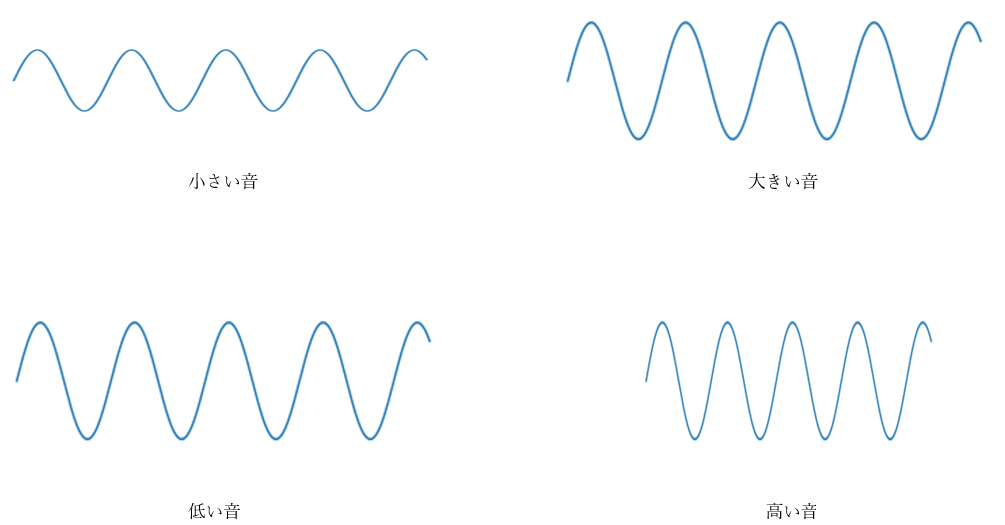
このグラフはオシロスコープと呼ばれる機械に音を流すことで発生させることができます。

音速

中学校の時に音速について勉強しましたよね。

さあ、音の速さを覚えているでしょうか？

上記のように習っていると思います。

高校物理ではもう少し踏み込んで勉強しましょう。

音速を表す公式は以下のように表します。

$$ V = 331.5 + 0.6t $$

\( V \) は音速を \( t \) は温度を表しています。

つまり音速は気温によって速さが変わるということなんですね。

夏場は音速が早く伝わり、冬場は夏に比べて遅くなる。我々人間の間隔では感じ取れるほどの違いではありませんが、確かに上記のような公式が成り立ちます。

中学生の時に習った340m/sというのは、外気温15℃を暗黙の内に決めていたんですね。

また、冒頭で音波の媒質は空気だと言いましたが、液体や固体中も音は伝わります。

しかも、気体よりも分子が密集しているため、音速は気体→液体→固体の順に早くなります。

音の重ね合わせ

前回は「重ね合わせの原理」について勉強しました。

音も波であることから「重ね合わせ」が存在します。

これはうなりと呼ばれる現象です。

振動数がわずかに異なる音同士を同時にならすと「ウァーン」「ウァーン」というような音が聞こえます。

この「わずかに異なる音」というのがポイントです。

振動数が大きくズレていると人間は、それぞれが違う音と認識できるためうなりは発生しません。

そんなうなりの公式ですが以下のようになります。

$$ f =| f_1 – f_2 | $$

\( f \) は1秒あたりのうなりの回数を \( f_1 \) と \( f_2 \) はそれぞれの音の振動数を表しています。

絶対値がついているのは、引き算したときにマイナスが出てこないようにするためです。

問題によっては \( f_1 \) と \( f_2 \) のどちらの振動数が大きいのかが分からない場合があります。

そんなときにいちいちマイナスを気にすることはめんどくさいので絶対値がついていると思ってください。

グラフは次のようになります。

振幅が大きいときに「ウァーン」と鳴って、振幅が小さいときに音が止んでいるイメージです。

ちなみにですが、このうなりという現象は楽器などの音を調律する際に利用されています。

例えば、とある楽器を600Hzに合わせたいとします。絶対音感を持っていれば別ですが、そうでない場合は、楽器の振動数が599Hzだったとしても聞き分けられません。

そこで600Hzの「おんさ」などを用意します。楽器を鳴らしてうなりが発生するようであれば、楽器の振動数がズレているということになりますよね？

うなりが無くなれば楽器の調律は終了です。

まとめ

今回は音について勉強しました。ポイントは以下の通りです。