今回は「加速度」について勉強していきます!
「加速」という言葉は聞き馴染みのない言葉ではないですが、物理基礎を勉強し始めた人に最初に立ちはだかる難所です。
一つ一つ丁寧に解説していきますので頑張っていきましょう!
加速度
さあ!いきなり出てきました!「加速度」です。
まずは定義を確認しましょう。
加速度:単位時間あたり(1秒あたり)の速度の変化量
これが加速度の定義です。
しっかり覚えましょう!
通常は \( a \) で表され、単位は \( m/s^2 \)(メートル毎秒毎秒)となります。
1秒間における速度の変化量だというのが重要です。
皆さんは「加速」と聞くとスピードを上げるイメージがありませんか?
間違ってはいませんが、物理基礎においては100点満点中50点の解答です。
速度の変化というのは何もスピードを上げることだけではありませんよね?
そうです。「減速」することも速度の変化です!
1秒間に2(m/s)スピードを上げれば \( a \) =2 \( m/s^2 \)
逆に1秒間に2(m/s)減速すれば \( a \) =-2 \( m/s^2 \) となります。
「加速」と「減速」も符号で区別するんですね!
加速度の公式
ここでは加速度の公式を示します。
正直なところ加速度の定義をしっかり理解している人にとっては、不必要なものであると思います。
しかし、初学者にとっては ”初め” はあった方がいいと思いますので次に示します。
$$ a = \frac{v’-v}{t’-t} $$
時間が \( t’ \)から \( t \) の間に速度が \( v’ \)から \( v \) に変化したという意味ですね!
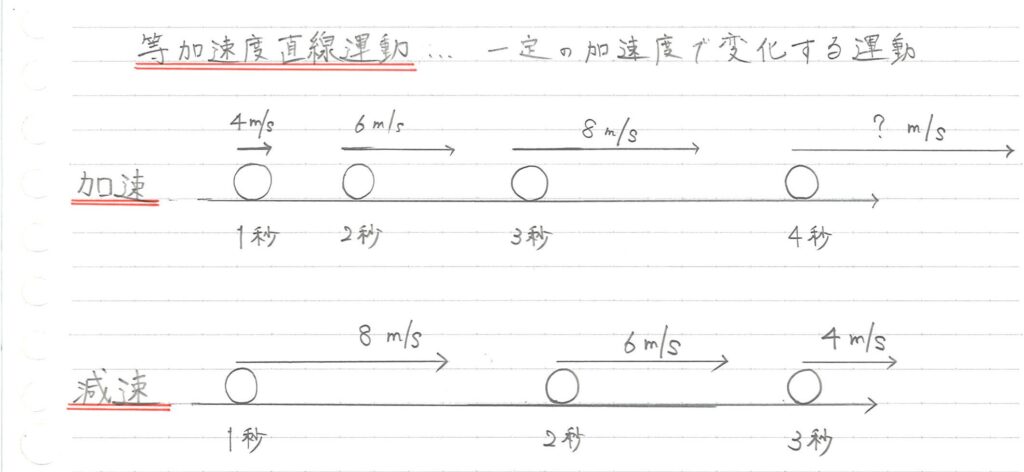
等加速度直線運動
加速度を理解したら次は等加速度直線運動です!
等速直線運動と似た言葉ですね。
そうです。同じように考えましょう。
等加速度直線運動:一定の加速度で変化する運動
つまり、一定の割合でスピードが上昇する、もしくは一定の割合でスピードが減少する運動のことです。
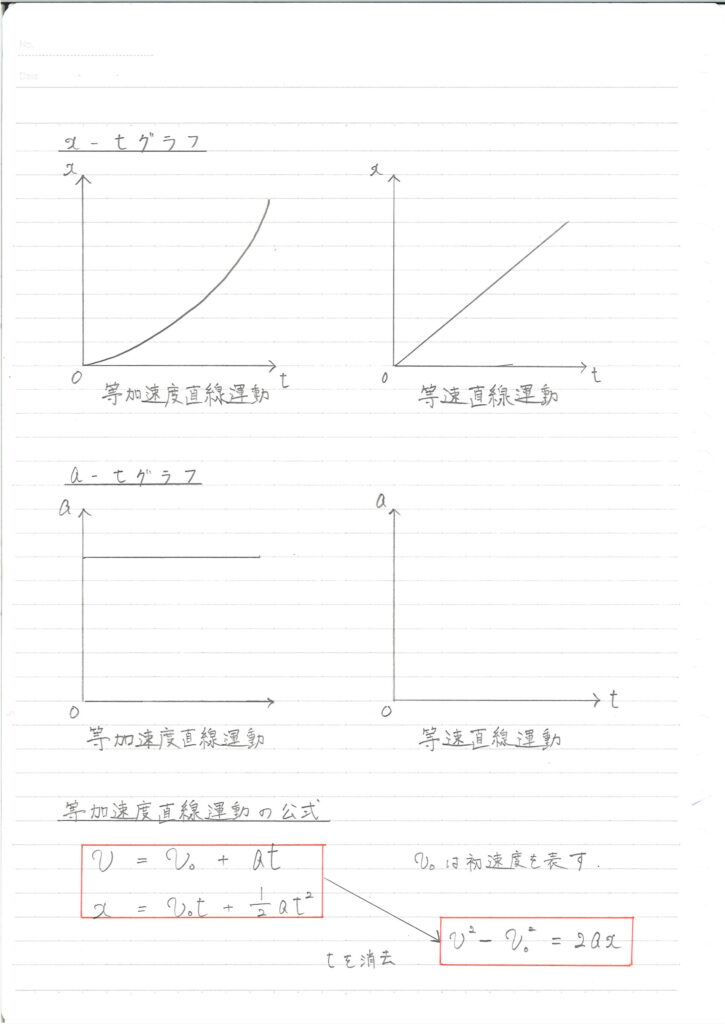
\( v-t \)グラフ
等加速度直線運動においても\( v-t \)グラフを考えましょう!
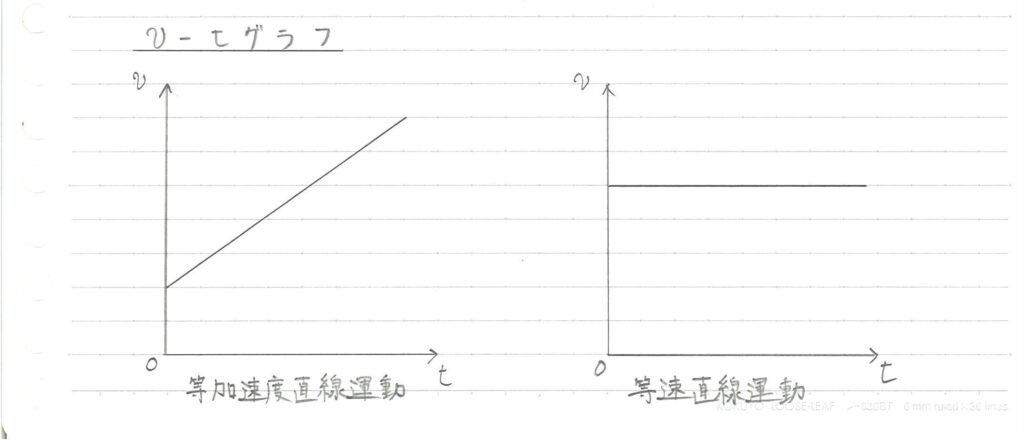
分かりやすいように、等速直線運動の場合の\( v-t \)グラフも示します。
等速直線運動では”速度が一定”だったのに対して、等加速度直線運動では”加速度が一定”なため、速度が一定の割合で変化していく一次関数のグラフになります。
\( x-t \)グラフ
次は\( x-t \)グラフについてです。
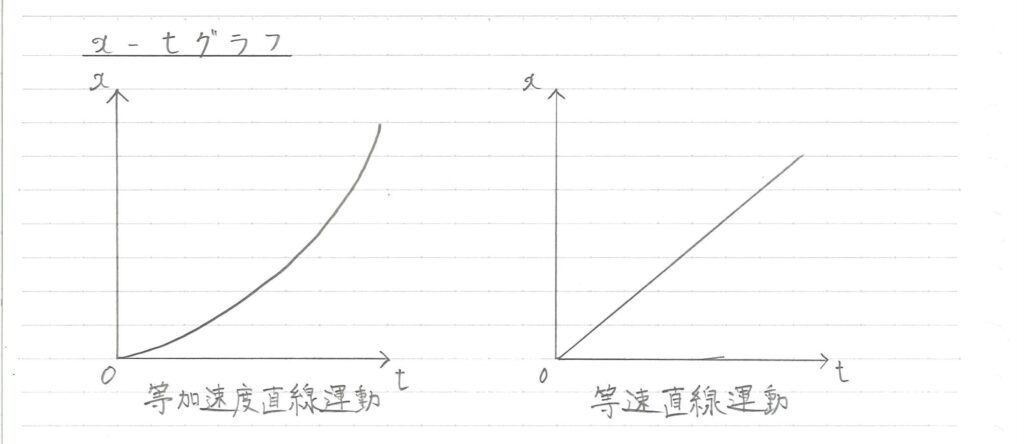
これも等速直線運動の場合と比べながら見ていきましょう!
等加速度直線運動の場合は、グラフが曲線になっていていかにもめんどくさそうですね。
\( a-t \)グラフ
最後は\( a-t \)グラフです。
これは等速直線運動には出てこなかったグラフですね。
一応等速直線運動の場合もグラフに示すことはできますが、あまり意味がないので普通は書きません。
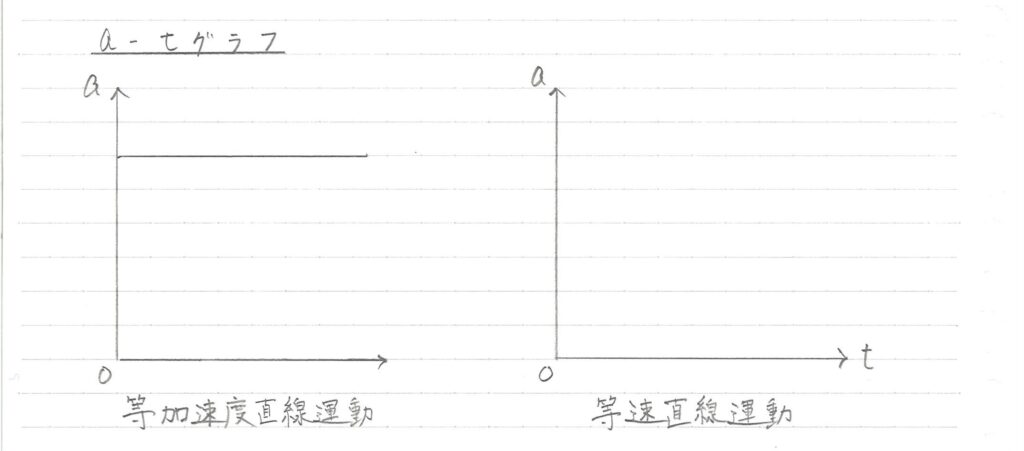
これも等速直線運動の場合と比べながら見ていきます。
\( a-t \)グラフはそんなに難しくはありません。
等加速度直線運動の場合は\( a \)が一定なので、横軸に平行なグラフになります。
等速直線運動の場合は、そもそも\( a \)が存在しないため0ですね。
等加速度直線運動を式で表す
それでは、等加速度直線運動を式で表してみましょう!
等速直線運動の場合はどうでしたか?
そうですね!「み・は・じ」の公式で全て解決できてましたね!
等加速度直線運動の場合はそうはいきません。
なぜか?それは当然「加速」するからです。
というわけで「み・は・じ」の代わりになる式を見つける必要がありそうですね!
はい!これです!
$$ v = v_0+at $$
$$ x = v_0t + \frac{1}{2}at^2 $$
それぞれ、速度と位置を表す公式になります!\( v_0 \)は初速を表しています。
\( x \)は単純な距離を表しているのではありません。
座標を表しているということに注意してください!つまり出た答えにマイナスがつくこともあります。
その場合は、基準の位置よりもマイナス方向の位置に物体があると解釈します。
これは実際に問題を解かなければ実感しにくいと思いますので、問題演習を各自でやってみてください。
証明は以下の通りです。
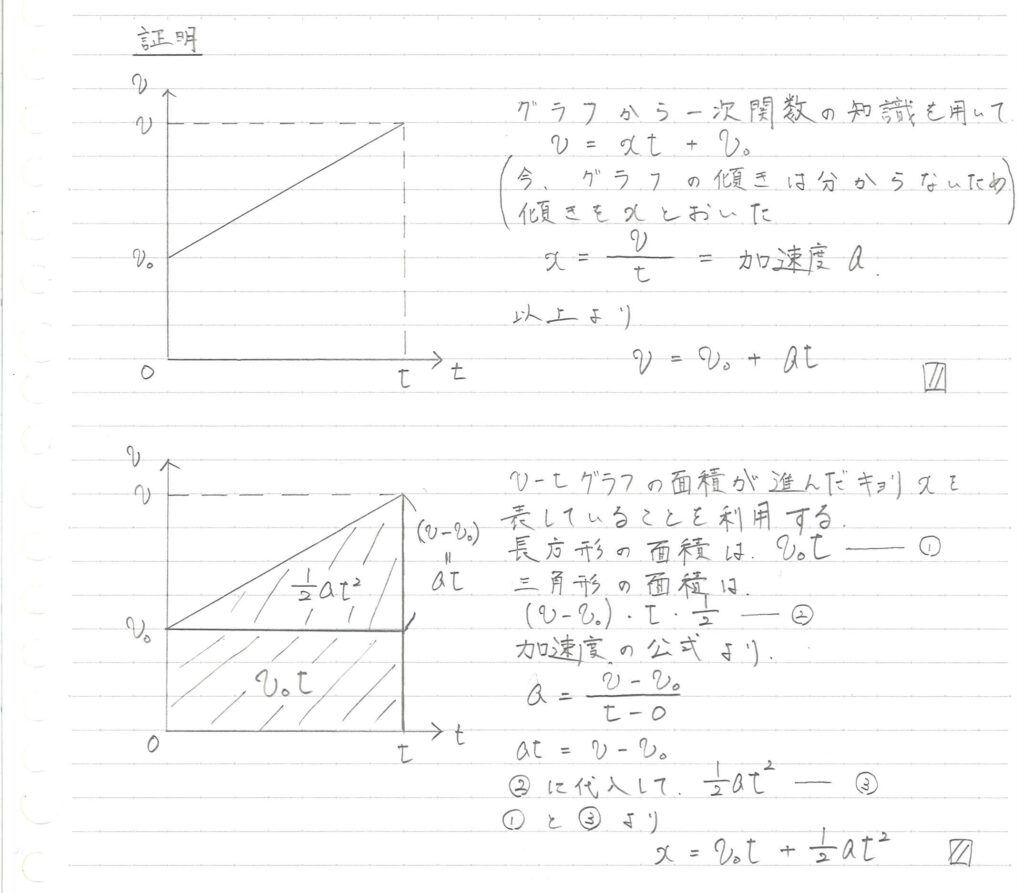
あと、この式も覚えておきましょう。
$$ v^2-v^2_0= 2at $$
これは上の2式から\( t \)を消すように連立させるとすぐに出ます。
問題文中に\( t \)が与えられていないときに重宝します。
まとめ

今回の内容は以上です。等加速度直線運動の公式はしっかり覚えておきましょう!
次回は、重力加速度について勉強します!



コメント