等速直線運動

はじめに

今日は力学の直線運動の世界について解説していきます！

そんなに難しい話ではないので頑張っていきましょう！

速さと速度の違い！？

皆さんは、速さと速度の違いを説明できますか？

「おんなじじゃん！」という声が聞こえてきそうですが、物理では明確に区別しています。

前回お話しした「定義を大切にする」ということがココでも言えます。

めんどくさがらずにちゃんと理解しましょう！

速さ：単位時間あたり（1秒間で）に進む道のり

速度：単位時間あたり（1秒間で）に進む道のりとその方向

わかりやすくするためにこんな書き方をしてみました。かえって分かりにくいかな？

簡単に言うと

速さ：向きを考慮しない

速度：向きまで考慮する

こんな違いです。速さに正と負の符号をつけて運動の向きを表すのです。

東向きを＋とすると「西向きに速さ80(km/h)」という表現を「速度-80(km/h)」と表現することができます。

以上のことから、速さは「スカラー」速度は「ベクトル」なんて言われたりします。

みはじの式

小学校で習った「みはじ」の式を覚えていますか？

道のり(距離)＝速さ×時間

でしたね。これを文字を使って表しましょう！

例えば道のり(距離)は “\( x \)”

速さ(or速度)は “\( v \)”

時間は “\( t \)”

でよく表されます。文字を使って「みはじ」を表すと

$$ x(m) = v(m/s)×t(s) $$

となりますね！

ここで前回の講義を思い出します。

物理で用いる単位は基本は「MKSA単位系」で表されるんでしたね！

長さの単位は（ｍ：メートル）

時間の単位は（s：秒）

速さの単位は（m/s：メートル毎秒）

となります！

なので今後 \( v \) と出てきたら、皆さんは「速さor速度」を表しているのだと思ってくださいね！

等速直線運動

次は等速直線運動についてです！

これは中学校の時に勉強した内容かと思います！

定義：速さも向きも変化しない運動を等速直線運動という

向きも考慮した速さを速度というので「速度の変化しない運動」と定義しても良さそうですね！

また「等速度運動」とも言うようですので覚えておきましょう！

さあ、ここからは等速直線運動をグラフに表していきたいと思います！

 \( x-t \) グラフ

まずは、 \( x-t \) グラフです。距離を縦軸に時間を横軸にとったグラフのことです。

ちなみにのお話ですが、今後はたくさんのグラフが出てきます。その際にグラフの様子から物体の運動を把握していかなければなりません。

最初は慣れないかもしれませんが、次のことを意識してください。

「縦軸と横軸が何を表しているのかを確認する」

これが最初にやるべきことです！

では実際に  \( x-t \) グラフを見ていきましょう！

これです！左側のグラフです！面食らうようであれば、

中学校数学でやった一次関数を思い出してください！右のグラフです！

$$ y = ax $$

切片がない一番簡単な関数ですね。

この式と見比べれば、  \( a \) と  \( v \) が対応していることが分かります。

つまり、速度 \( v \) は \( x-t \) グラフにおける傾きなのです！

傾きは「急」な程その値が大きく「緩やか」な程その値が小さくなるんでしたね。

そのことと対応させると、 \( x-t \) グラフが急なほど、速い運動を緩やかなほど、遅い運動をしていることが分かってしまうわけです！

よろしいでしょうか？

 \( v-t \) グラフ

次は \( v-t \) グラフです。これは速度を縦軸に時間を横軸にとったグラフのことです。

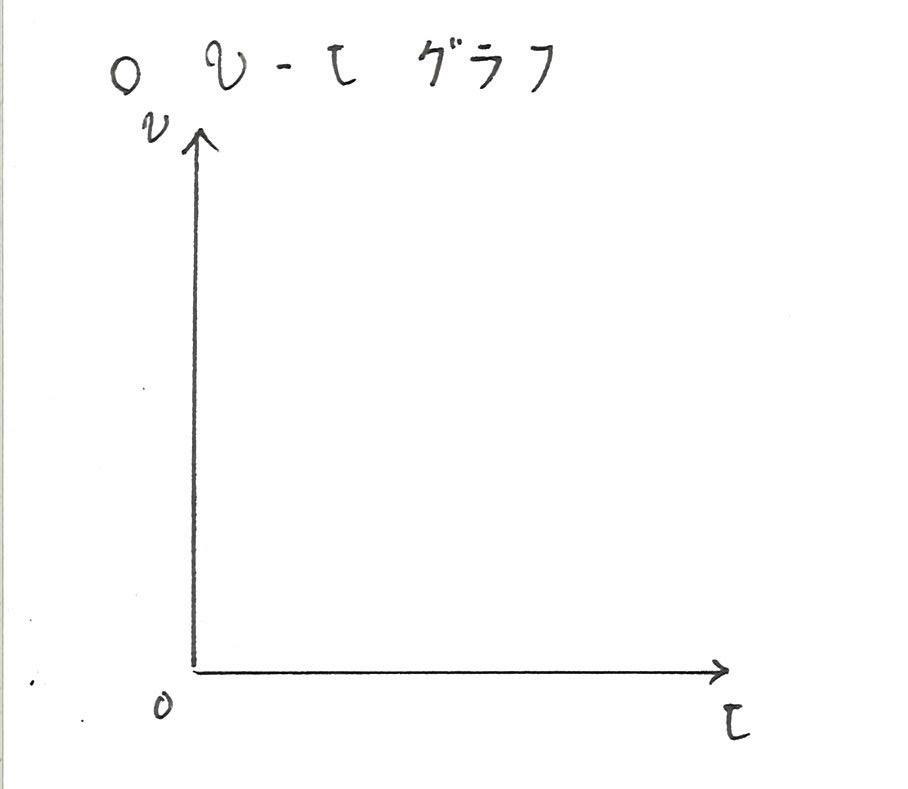
図のような \( v-t \) グラフがあった場合、等速直線運動を表すにはどのような直線を引けばいいか分かるでしょうか？

少し考えてみてください。

答えはこんな直線です。

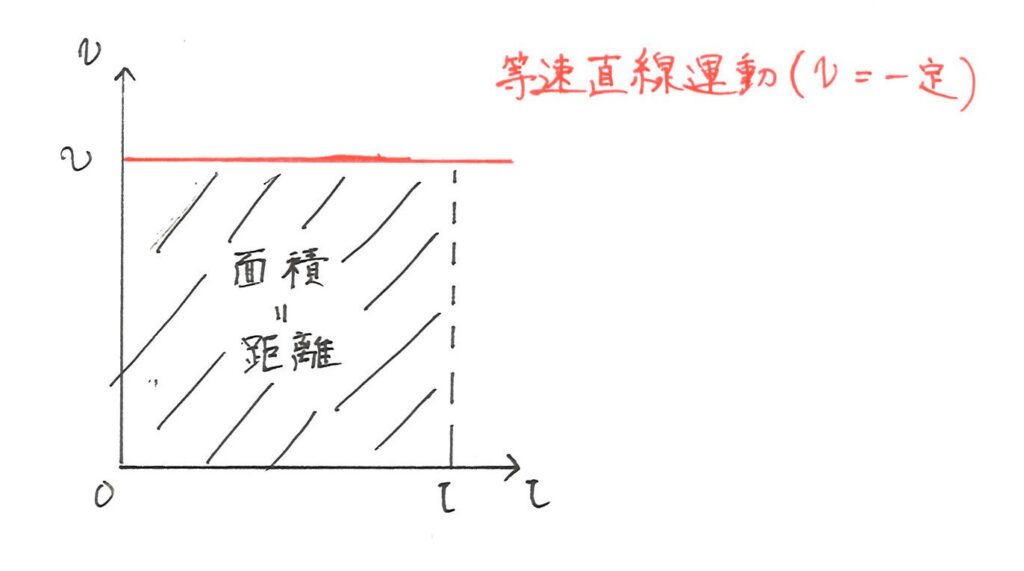
等速直線運動なので、速度 \( v \) は一定になりますね！

また「みはじ」の公式から \( v-t \) グラフの面積が進んだ距離 \( x \) を表す量になることが分かります。

これはめちゃくちゃ分かりやすいですよ！

難関大学に合格したい方におすすめの『まなぶてらす』

最近では勉強動画やブログのおかげで1人でも勉強できる環境がかなり整ってきてますよね！

それでも、分からない部分に多くの時間がかかってしまう時ってありませんか？

勉強を進めていて、こんな風にお悩みの方におすすめなのが

勉強と習い事が学べる総合型オンライン家庭教師『まなぶてらす』です。

『まなぶてらす』なら、どこからでもアクセスでき、難関大学の現役大学生や受験のプロが難しい質問にも答えてくれるだけではなく受験でのテクニックやポイントも教えてくれるため効率的に勉強できますよ！

また、オンラインサービスなので、２４時間３６５日のレッスンを実施しています。

夕方から夜はもちろん、早朝、平日昼（不登校児も受講可）、土日祝日、GW、お盆、年末年始など、毎日実施しています。

そのため、それぞれの生活リズムに合わせて利用してもらうことができます！

また『まなぶてらす』は勉強したい指導分野に強い講師を自分で選んで、指名することができます！

なかなか選べないという方にはメールやガイダンスサービスで講師を紹介してもらうことも可能です。

先生の話し方や雰囲気は、まなぶてらすのYoutubeチャンネルで確認することもできます。

✔『まなぶてらす』の特徴

『まなぶてらす』には、なんと初回無料レッスンがあります。

実際の指導と同様にみっちり指導を無料で受けることができます！

お金がかかるわけではないので、まずは実際の指導を受けてみて下さい！

大学入試の制度は年々変化しています。難関大学卒の講師であっても、現状を理解し切れていない部分があるかもしれません。

その点『まなぶてらす』の講師陣の中には東京大学をはじめとした難関大学の現役生が在籍しています。

今の受験制度を誰よりも知っていると言えます。

難関大学を狙っているけれども何から勉強すればいいのか分からない方などは是非、無料レッスンからでも利用してみて下さい！

まとめ

今回は \( x-t \) グラフと \( v-t \) グラフについて勉強しました。

この二つのグラフは今後も出てくるので必ず覚えてください！

次は、苦手意識を持つ人が多い「加速度」について勉強していきます。