力学におけるさまざまな力

はじめに

今回は、さまざまな力についてです。

前回の記事で、物理において力と呼ぶものについてお話ししました。

こんかいはそれらを1つずつ説明していきます。

はじめに

まずは単位を確認しましょう。

力の単位を覚えていますか？

N：ニュートンでしたね。

ただ、このN（ニュートン）という単位は、簡単に1文字で表すことができるように導入された単位です。

では、力の単位とはどんな形をしているのでしょうか？

運動方程式を思い出してください。

$$ ma = F $$

質量 \( m \) の単位は kg(キログラム) 加速度\( a \) の単位は \( m/s^2 \)(メートル毎秒毎秒)でした。

つまり 力を表す単位である N（ニュートン）は、本当は \( kg・m/s^2 \) ということだと分かります。

今後は \( kg・m/s^2 \) という単位になればそれは物理的に力だと認めてよいことになりますね。

重力

重力は質量 \( m \) と重力加速度 \( g \) の掛け算で表します。

\( mg \) ですね。

これは先ほど確認した運動方程式と同じですね。　

重力に似たものとして万有引力もあります。

万有引力も力です。

重力と万有引力は日常生活レベルであれば同じものとして考えていいのですが、物理的には微妙に異なるものです。

この辺はもう少し先で扱いましょう。

重力 \( mg \) ですが、これは普段みなさんが体重計に乗った時に表示される値です。

あなたの質量 \( m \) に地球の重力加速度 \( g \) が掛けられた値が、あなたの体重として表されます。

なんか変じゃないですか？

だって、体重計で表示される値の単位は kg ですよね。

でも、今見てきた通り \( mg \) の単位は N です。

おかしいですよね？

これは「重さ」と「質量」の違いにあります。

「重さ」はいわゆる「重力」のことだと思ってください。

だから \( mg \) です。体重計で表される値はみんなの「重さ」を表しています。

質量は \( m \) を表しています。

だから物理的に細かく指摘すれば、体重計の値は N という単位で表されるべきなんですね！

地球の重力加速度 \( g \) は 9.8 であることが実験的に分かっています。

これは重要な値なので覚えてください。

もし、皆さんが自分の本当の「質量」を知りたいのであれば、体重計の値を 9.8 で割ってください。

それが、あなたの本当の「質量」になります。

これは中学校理科でも扱いますかね？

月に行けば「重さ」は６分の１になるが「質量」は変わらないよっていう話です。

ここら辺もややこしいのですが、要するに月の重力加速度が地球の６分の１だから「重さ」も６分の１になるよね、という話なんです。

摩擦力

次は摩擦力です。

摩擦力は日常でもよく関わりのある力ですね。

車や自転車のブレーキも摩擦によるものですからね。

そんな身近な摩擦力ですが「なぜ摩擦が発生するのか」という本質的な部分は実はまだ分かっていないそうなんですよ。

不思議ですよね。

摩擦力には大きく分けて２種類あります。

同じ摩擦ですが２種類あります。

動摩擦力

動摩擦力は「物体を動かしている時に発生している摩擦力」のことです。

$$ F’ = μ’N $$

動摩擦力は上記の式で表します μ’ は「動摩擦係数」と呼ばれるもので、物体と床との滑りにくさを表す物理量です。

単位はありません。

\( N \) は以前出てきましたね。

垂直抗力です。要は物体の「重さ」のことですね。

つまり、物体と床との滑りにくさと物体の重さで摩擦力は決まるということです。

静止摩擦力

静止摩擦力は「静止している物体を動かそうとするときに発生する摩擦力」のことです。

また、静止している物体が動き出すか動き出さないギリギリの部分での摩擦力を「最大静止摩擦力」と言います。

静止摩擦力を表す式は動摩擦力の時と一緒です。

$$ F = μN $$

動摩擦力は上記の式で表します。

μ は「静止擦係数」と呼ばれるもので、物体と床との滑りにくさを表す物理量です。

単位はありません。

\( N \)は垂直抗力です。

動摩擦力と静止摩擦力の違い

動摩擦力と静止摩擦力は何が違うのでしょうか？ココでは結果のみ述べます。

動摩擦力<静止摩擦力

という関係があります。

つまり、静止摩擦力の方が動摩擦力よりも大きいのです。

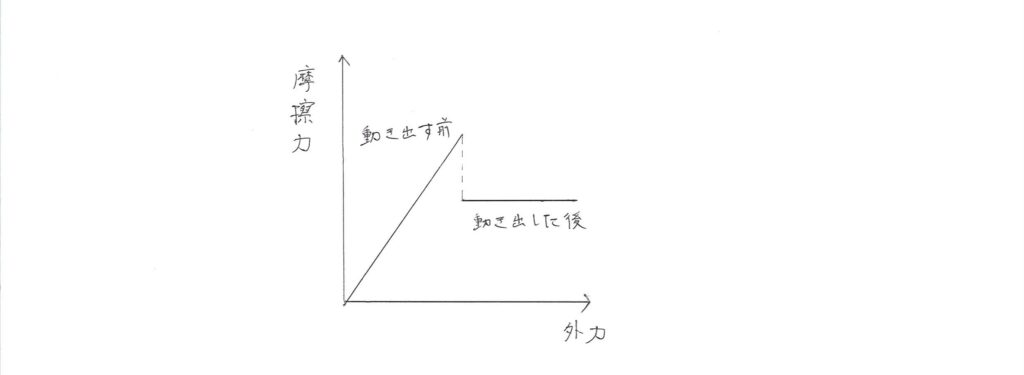
重いものを動かすときに動かすまでは大変で動き出したらサクサク動いたという経験はありませんか？

それは上記の静止摩擦力の方が動摩擦力よりも大きいことが原因です。

グラフで示すと次のようになります。

摩擦のもう少し深い話

高校物理の教科書には載っていないので、興味がなければココはスルーしてください。

高校物理の範囲で考える摩擦には次のような法則もあります。

そもそも摩擦力の研究は紀元前のエジプトまで遡る程、歴史が古いのです。

ピラミッドを作るために大きくて思い石を運ぶ必要があったため、当然と言えば当然かもしれませんね。

しかし、紀元前から研究されているにもかかわらず、摩擦力は未だに分かっていないことが多いのです。

また、上記に示した法則や高校物理の範囲での摩擦は限定的な理解です。

地球規模の摩擦（例えば地震など）や原子スケールでの摩擦を考える際は、上記の法則は必ずしも当てはまるとは限りません。

また、静止摩擦力は時間が経てば経つほど大きくなるらしいです。

ただ、摩擦力の増加は対数的に増加していくらしいので、限度はありますね。

長年放置しているタンスの静止摩擦力が無限大に（言いすぎかな）大きくなるかと言えば、そういうわけではないんですね。

浮力

浮力も日常に深い関係がありますね。

プールやお風呂に入ると体が軽くなります。

あれは浮力のおかげです。

浮力は次のような式で表されます。

$$ F = ρVg $$

\( ρ \)は流体の密度を表します。単位は \( kg/m^3 \) です。

\( V \)は物体の体積を表します。単位は \( m^3 \) です。

複雑ですが単位を自分で整理してみてください。\( kg・m/s^2 \) になるはずです。

浮力の定義は次のようなものです。

浮力は液体中にある物体の体積分の液体の重さに等しい

難しいですよね。

浮力って最初はすごく難しいのです。

これを理解するにはアルキメデスの原理を理解する必要があります。

アルキメデスの原理

アルキメデスの原理は次のような原理です。

物体にはたらく浮力は、物体が押しのけた流体の重さに等しい

これも意味が分かりにくいですよね。

詳しく説明します。

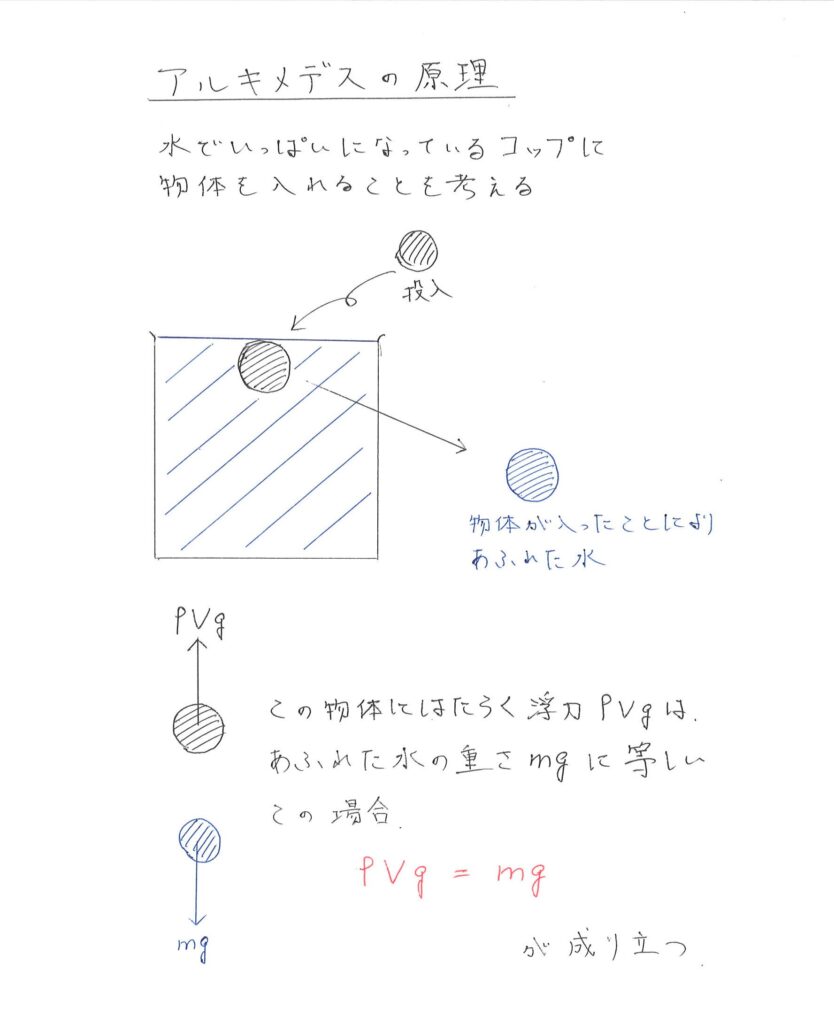
コップに満杯に水が入っているとします。

ここに氷を１つ入れます。

そうするとどうなるでしょうか？

当然、入った氷の分だけ水があふれます。

そして氷は水に浮きますね。

この氷にはたらく浮力は、先ほどあふれた水の重さと同じだというのがアルキメデスの原理です。

アルキメデスはその昔、お風呂に入っている時にこの原理を思いついたと言われています。

この時にうれしさのあまり、素っ裸で外に出て「エウレカ！エウレカ！」（ギリシャ語でやったぞ！）と叫びまわったという話もあるくらいです。

実際にアルキメデスは自身のアルキメデスの原理を用いて、王冠が純金かどうかを見破ったそうです。

先ほどの浮力に戻ります。

結局は、浮力で示した定義とアルキメデスの原理は同じような意味なんですね。

つまりは下記のようになります。

物体にはたらく浮力＝物体が押しのけた流体の重さ

$$ ρVg＝mg $$

浮力の式を見てみると流体の密度 \( ρ \) が大きいほど、物体の体積 \( V \) が大きいほど物体にはたらく浮力は大きくなります。

そのため、水銀のような高密度の液体には、ボルトやナットのような金属が浮きます。

まとめ

今回はさまざまな力についてでした。

今回示した力は次の通りです

特に浮力は定義をしっかり理解しておきましょう。